|
The Reuleaux Triangle Tetrahedron:
 The Reuleaux Triangle
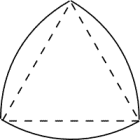
Reuleaux Triangle The Reuleaux triangle is the simplest nontrivial example of a curve of constant width - a curve in which the distance between two opposite parallel tangent lines to its boundary is the same, regardless of the direction of those two parallel lines. The Reuleaux Tetrahedron

Reuleaux Tetrahedron The sphere through each vertex passes through the other three vertices, which also form vertices of the Reuleaux tetrahedron. The Reuleaux tetrahedron has the same face structure as a regular tetrahedron, but with curved faces: four vertices, and four curved faces, connected by six circular-arc edges. In contrast to the Reuleaux Triangle it does not have constant width. The Reuleaux Triangle Tetrahedron

Reuleaux Triangle Tetrahedron The Applet shows the polyhedron with colored Reuleaux Triangles. Use the left mouse button to rotate the object. The "e" key centers the tetrahedron. The applet was written by Stefan Sechelmann a member of the Research Group Polyhedral Surfaces. For the general construction method see A. I. Bobenko, I. Izmestiev. Alexandrov's theorem, weighted Delaunay triangulations, and mixed volumes. Preprint arXiv:math.DG/0609447, 2006. Stefan Sechelmann 11-15-2006 |
